هندسه وصفيه
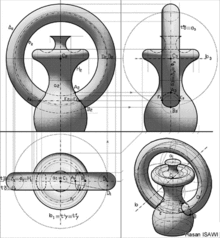
الهندسة الوصفية هيا فرع من فروع الهندسة يسمح بتمثيل الأجسام ثلاثية الأبعاد فى بعدين باستخدام مجموعة محددة من الإجراءات. تعتبر التقنيات الناتجة مهمة للهندسة والهندسة المعمارية والتصميم والفن .[1] يتم توفير الأساس النظرى للهندسة الوصفية منفىالإسقاطات الهندسية المستوية . أول منشور معروف عن دى التقنية كان "Underweysung der Messung mit dem Zirckel und Richtscheyt" ( ملاحظة القياس باستخدام البوصلة ومستوى الروح )، نُشر فى لينين، نورمبرغ: 1525، بواسطة ألبريشت دورر . كان المهندس المعمارى الإيطالى غوارينو جوارينى كمان رائدًا فى الهندسة الإسقاطية والوصفية، من كتابه Placita Philosophica (1665)، وإقليدس أدوكتوس (1671)، و Architettura Civile (1686 - لم يُنشر لحد 1737)، متوقع أعمال غاسبار مونج (1746). -1818)، اللى يُنسب ليه اختراع الهندسة الوصفية.[2] يعتبر غاسبار مونج "أبو الهندسة الوصفية" نظر تطوراته فى حل المشكلات الهندسية. كانت اكتشافاته الأولى سنة 1765 لما كان يعمل رسام للتحصينات العسكرية، رغم نشر النتائج اللى توصل ليها بعدين .[3] تسمح بروتوكولات مونج برسم كائن وهمى بطريقة ممكن تشكيلها فى 3 أبعاد. يتم حساب كل الجوانب الهندسية للكائن الوهمى بالحجم الحقيقي/المقياس والشكل الحقيقيين، ويمكن تصويرها كما تُرى من أى موضع فى الفضاء. يتم تمثيل كافة الصور على سطح ثنائى الأبعاد.
بروتوكولات[تعديل]
- إسقط صورتين لجسم ما فى اتجاهات عشوائية متعامدة. يستوعب كل عرض للصورة 3 أبعاد للمساحة، يتعرض بعدين كمحاور كاملة الحجم ومتعامدة بشكل متبادل وواحد كمحور غير مرئى (عرض نقطي) يتراجع فى مساحة الصورة (العمق). تشترك طريقتى عرض الصور المتجاورتين فى عرض كامل النطاق لواحد من أبعاد الفضاء الثلاثة.
- ممكن تكون أى من الصور دى نقطة بداية لعرض تالت متوقع. قد يبدأ الرأى التالت بإسقاط رابع، و لما لا نهاية. يمثل دى الإسقاطات المتسلسلة دوران دائرى بزاوية 90 درجة فى الفضاء علشان رؤية الجسم من اتجاه مختلف.
- يستخدم كل إسقاط جديد بُعدًا بالحجم الكامل يظهر كبُعد وجهة نظر فى العرض السابق. لتحقيق العرض الكامل لده البعد واستيعابه ضمن العرض الجديد يتطلب تجاهل العرض السابق والانتقال لالعرض السابق التانى حيث يظهر ده البعد بالحجم الكامل.
- ممكن إنشاء كل عرض جديد عن طريق الإسقاط فى أى مالوش حصر من الاتجاهات، بشكل عمودى على اتجاه الإسقاط السابق. (تخيل الاتجاهات الكتيرة لقضبان عجلة العربة، كل واحد منها متعامد مع اتجاه المحور.) النتيجة هيا التحرك بشكل دائرى حول جسم ما بزاوية 90 درجة وعرض الجسم من كل خطوة. تتم إضافة كل عرض جديد كعرض إضافى لشاشة عرض تخطيط الإسقاط الإملائى ويظهر فى "نموذج الصندوق الزجاجى المطوي".
بصرف النظر عن التصميم التعامدي، هناك ستة طرق عرض أساسية قياسية (قدامي، الجانب الأيمن، الجانب الأيسر، أعلى، أسفل، خلفي)، تسعى الهندسة الوصفية لإنتاج 4 طرق عرض أساسية للحل: الطول الحقيقى للخط (أى الحجم الكامل، مش التقصير) ، وعرض النقطة (عرض النهاية) للخط، والشكل الحقيقى للمستوى (أى الحجم الكامل للقياس، أو عدم تقصيره)، وعرض حافة المستوى (أى عرض مستوى مع خط الرؤية عمودى على خط البصر المرتبط بخط البصر لإنتاج الشكل الحقيقى للطائرة). فى الغالب ما تعمل دى على تحديد اتجاه الإسقاط للعرض اللاحق. منفىعملية التدرج الدائرية بزاوية 90 درجة، الإسقاط فى أى اتجاه من وجهة نظر الخط يؤدى لعرض الطول الحقيقى ؛ يؤدى الإسقاط فى اتجاه موازٍ لعرض خط الطول الحقيقى لعرض النقطة الخاصة به، كما يؤدى عرض النقطة لأى خط على المستوى لعرض حافة المستوى؛ سيؤدى الإسقاط فى اتجاه عمودى على عرض حافة المستوى لعرض الشكل الحقيقى (للقياس). قد يتم استدعاء وجهات النظر المختلفة دى للمساعدة فى حل المشكلات الهندسية اللى تطرحها مبادئ الهندسة الصلبة
الاستدلال[تعديل]
هناك قيمة إرشادية لدراسة الهندسة الوصفية. إنه يعزز التصور والقدرات التحليلية المكانية، فضل عن القدرة البديهية على التعرف على اتجاه الرؤية لتقديم احسن مشكلة هندسية للحل. أمثلة تمثيلية:
حلول عامة[تعديل]
الحلول العامة هيا فئة من الحلول ضمن الهندسة الوصفية اللى فيها كل الحلول الممكنة لمشكلة ما. يتم تمثيل الحل العام بجسم واحد ثلاثى الأبعاد، فى العاده ما يكون مخروطًا، وتكون اتجاهات عناصره هيا اتجاه العرض المطلوب (الإسقاط) لأى عدد لا حصر له من طرق عرض الحل.
شوف كمان[تعديل]
مصادر[تعديل]
- ↑ Joseph Malkevitch (April 2003), "Mathematics and Art", Feature Column Archive, American Mathematical Society
- ↑ Bianchini, Carlo (2012). "Stereotomy Role in Guarino Guarini's Space Research". Nuts and Bolts of Construction History. 1: 257–263. ISBN 978-2-7084-0929-3.
- ↑ Ingrid Carlbom, Joseph Paciorek (December 1978), "Planar Geometric Projections and Viewing Transformations", ACM Computing Surveys, 10 (4): 465–502, doi:10.1145/356744.356750
